高中数学函数最值问题的多解法对比与优化策略研究

高中数学函数最值问题的多解法对比与优化策略研究

李健丰

浙江省柯桥中学 邮编：312030

摘要：本文探讨函数最值问题的求解。函数最值问题求解对深化函数性质理解、培养数学思维能力及提升实际应用能力意义重大。常见解法有代数法、几何法和导数法，各有适用场景与优缺点。当前教学中，存在学生解法选择缺乏针对性、忽视定义域限制，以及教师解法教学缺乏系统性、实际应用问题涉及较少等问题。对此，可通过单调性分析定最值、数形结合直观化、导数工具破疑难等策略优化求解，以提高函数最值问题求解的效率与准确性，帮助学生更好掌握相关知识与技能。

关键词：函数最值；多解法；对比分析；优化策略

一、函数最值问题求解的重要性

函数最值问题求解意义重大。首先，它有助于深化对函数性质的理解。函数最值和单调性、奇偶性等性质紧密相连，求解最值能让学生更直观地把握函数变化规律，进而深入理解函数概念本质。其次，对培养数学思维能力大有裨益。求解函数最值问题需要综合运用代数运算、几何直观、逻辑推理等多种思维，像利用导数求最值体现极限思想，借助几何图形转化问题体现数形结合思想，能有效培养学生的抽象、发散与综合思维能力。最后，还能提升实际应用能力。在物理、经济、工程等众多领域，许多实际问题都能转化为函数最值问题，求解可让学生感受数学的实用价值，增强运用数学知识解决实际问题的本领。

二、函数最值问题的常见解法及对比

函数最值问题常见三种解法。代数法，通过配方、不等式、方程等代数运算求解，适用于二次函数等简单函数，逻辑严谨、步骤明确，对典型函数求解效率高，但对复杂函数运算繁琐、易出错。几何法基于函数几何意义，用图像或模型转化问题，常见于线性规划等场景，直观形象，能降低思维难度，不过受函数图像复杂性限制，对高次、非初等函数适用性窄。导数法利用导数与函数单调性关系，通过求导找极值点确定最值，适用于可导函数，普适性强，能解决多数连续函数最值问题，但计算过程复杂，对导数求解准确性要求高，还需结合定义域判断极值与最值关系，对学生逻辑严谨性要求较高。

三、函数最值问题求解的现状

在函数最值问题教学中，存在学生和教师两方面的问题。一方面，学生解法选择缺乏针对性。部分学生对不同解法的适用条件认识模糊，在解题时不能根据函数特点合理选择解法，盲目运用不恰当的方法，增加了计算量甚至无法求解。而且，学生常忽视定义域对最值的限制，导致结果出错。另一方面，教学层面解法教学缺乏系统性。部分教师教学时过于侧重单一解法，强调某一种解法的优势，却忽略其他解法的思维培养。在对比不同解法时，也未对适用场景进行有效归纳，学生难以建立解法与问题的联系。此外，教学中实际应用问题涉及较少，学生难以将所学方法运用到实际场景中。

四、函数最值问题求解的优化策略

（一）单调性分析定最值

利用函数单调性来确定最值，是解决函数最值问题最基础且常用的办法。对于连续函数而言，若在定义域里有单调递增或者递减的区间，那最值通常就出现在区间的端点，或者是单调性发生改变的转折点处。具体解题时，需要先判断函数单调性。可以用求导的方法，也能根据函数单调性的定义来判断。判断出单调性之后，再结合函数的定义域，就能确定最值可能出现的位置了。例如，求函数f(x)=x3−3x+1在区间[−2,2]上的最值，先求导得f(x)=3x2−3，令导数为零，解出x=±1。接着分析单调性，在(−2,−1)函数递增，(−1,1)递减，(1,2)又递增。最后算出区间端点和极值点的函数值，f(−2)=−1，f(−1)=3，f(1)=−1，f(2)=3，这样就能得出最大值是3，最小值是−1。

（二）数形结合直观化

借助函数图像的几何特征来分析最值问题，能把抽象的代数关系变成直观的图形，这样理解起来更容易，像二次函数、三角函数等具有明显图像特征的函数类型。通过观察图像的顶点、最高点、最低点等关键位置，就能快速找出最值。以二次函数f(x)=−x2+2x+3为例，求其在区间[0,3]上的最值。该函数的图像是开口向下的抛物线，对称轴是x=1。根据二次函数图像性质，开口向下时，对称轴对应的函数值就是最大值，算出来f(1)=4。再看区间端点，f(0)=3，f(3)=0，显然最小值是0。通过画图像，可以直接看到抛物线在这个区间内的升降趋势，无需复杂计算即可判断最值位置。

（三）导数工具破疑难

在面对复杂函数或者含有参数的最值问题时，导数是特别强有力的求解工具。利用导数，能够深入分析函数的极值点、单调递增的。再结合函数本身的定义域，可以系统且准确地解决各种各样的最值问题。这种方法对于高次函数、分式函数，还有三角函数与指数对数函数组合而成的复合函数等，都十分适用。例如，求函数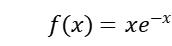在定义域R上的最值，先求导算出f(x)，令其为零得到x=1。通过分析导数正负判断单调性，能确定x=1是极大值点也是最大值点，进而算出最大值。结合函数在正负无穷的趋势，就能判断出有无最小值。

结论

函数最值问题求解对理解函数性质、培养思维能力及提升实际应用能力意义显著。当前教学中，学生存在解法选择不当、忽视定义域等问题，教学层面则解法教学缺乏系统性、实际应用涉及少。优化需从三方面入手：利用单调性分析，结合定义域确定最值位置；借助数形结合，将抽象关系转化为直观图形判断；运用导数工具，分析复杂函数极值与单调性以求解。通过针对性策略，可提升学生解题效率与应用能力，完善教学效果。

参考文献

[1]李春林.一题多解“细”探究巧构函数“觅”思路——一道以函数为背景的不等式恒成立问题的多解法探究[J].数理化解题研究,2023,(25):85-88.

[2]吴愉薇.波利亚解题思想在高一函数最值问题教学中的优化研究[D].广州大学,2023.